Matematica

SimpleInterest loop math interactive Livello 8

Scrivi il programma SimpleInterest utile per calcolare l’interesse semplice di un prestito. Il programma deve funzionare nel modo seguente:

Chiede di inserire il capitale iniziale ( $C = M_{0}$ )
Se il valore inserito non è un numero valido stampa il messaggio:
```
 Valore C non valido "<valore>"   e ricomincia dal punto 1.
```

Se il valore inserito è inferiore o uguale 0 stampa:

 C deve essere maggiore di 0   e ricomincia dal punto 1.

Chiede di inserire il tasso di interesse ( $i$ )

Se il valore inserito non è un numero stampa:

 Valore i non valido "<valore>"   e ricomincia dal punto 4.

Chiede di inserire il periodo ( $n$ )

Se il valore inserito non è un numero intero stampa:

 Valore n non valido "<valore>"   e ricomincia dal punto 6.

Se il valore inserito è inferiore a 0 stampa:

 Il periodo deve deve essere positivo  e ricomincia dal punto 6.

Stampa il montante ( $M_{n}$ ) del prestito

Esempio 1:

Inserire il capitale iniziale (C): 1000
Inserire il tasso di interesse (i): 5
Inserire il periodo (n): 2
M2 = 1100.0

Esempio 2:

Inserire il capitale iniziale (C): -1
Il capitale deve essere maggiore di 0
Inserire il capitale iniziale (C): bau
Valore C non valido "bau"
Inserire il capitale iniziale (C): 1000
Inserire il tasso di interesse (i): miao
Valore i non valido "miao"
Inserire il tasso di interesse (i): 7
Inserire il periodo (n): -1
Il periodo deve essere positivo
Inserire il periodo (n): cucu
Valore n non valido "cucu"
Inserire il periodo (n): 5
M5 = 1350.0

ArithmeticProgression math loop interactive Livello 8

Scrivi il programma ArithmeticProgression utile per calcolare i termini di una progressione aritmetica. Il programma deve funzionare nel modo seguente:

Chiede di inserire il valore del primo termine ( $a_{1}$ )
Se il valore inserito non è un numero intero stampa il messaggio:
```
 Valore a1 non valido "<valore>"   e ricomincia dal punto 1.
```
Chiede di inserire la ragione ( $r$ )

Se il valore inserito non è un numero intero stampa:

 Valore r non valido "<valore>"   e ricomincia dal punto 3.

Chiede di inserire il numero di termini da stampare (N)

Se il valore inserito non è un numero intero stampa:

 Valore N non valido "<valore>"   e ricomincia dal punto 5.

Se il valore inserito è inferiore a 1 stampa:

 Il numero di termini deve essere maggiore di 0   e ricomincia dal punto 5.

Stampa i primi N termini della progressione aritmetica

Esempio 1:

Inserire primo termine (a1): 1
Inserire ragione (r): 2
Inserire numero di termini (N): 10
1, 3, 5, 7, 9, 11, 13, 15, 17, 19.

Esempio 2:

Inserire primo termine (a1): bau
Valore a1 non valido "bau"
Inserire primo termine (a1): 1
Inserire ragione (r): miao
Valore r non valido "miao"
Inserire ragione (r): 2
Inserire numero di termini (N): muhh
Valore N non valido "muhh"
Inserire numero di termini (N): 0
Il numero di termini deve essere maggiore di 0
Inserire numero di termini (N): 5
1, 3, 5, 7, 9.

Cylinder methods math Livello 9

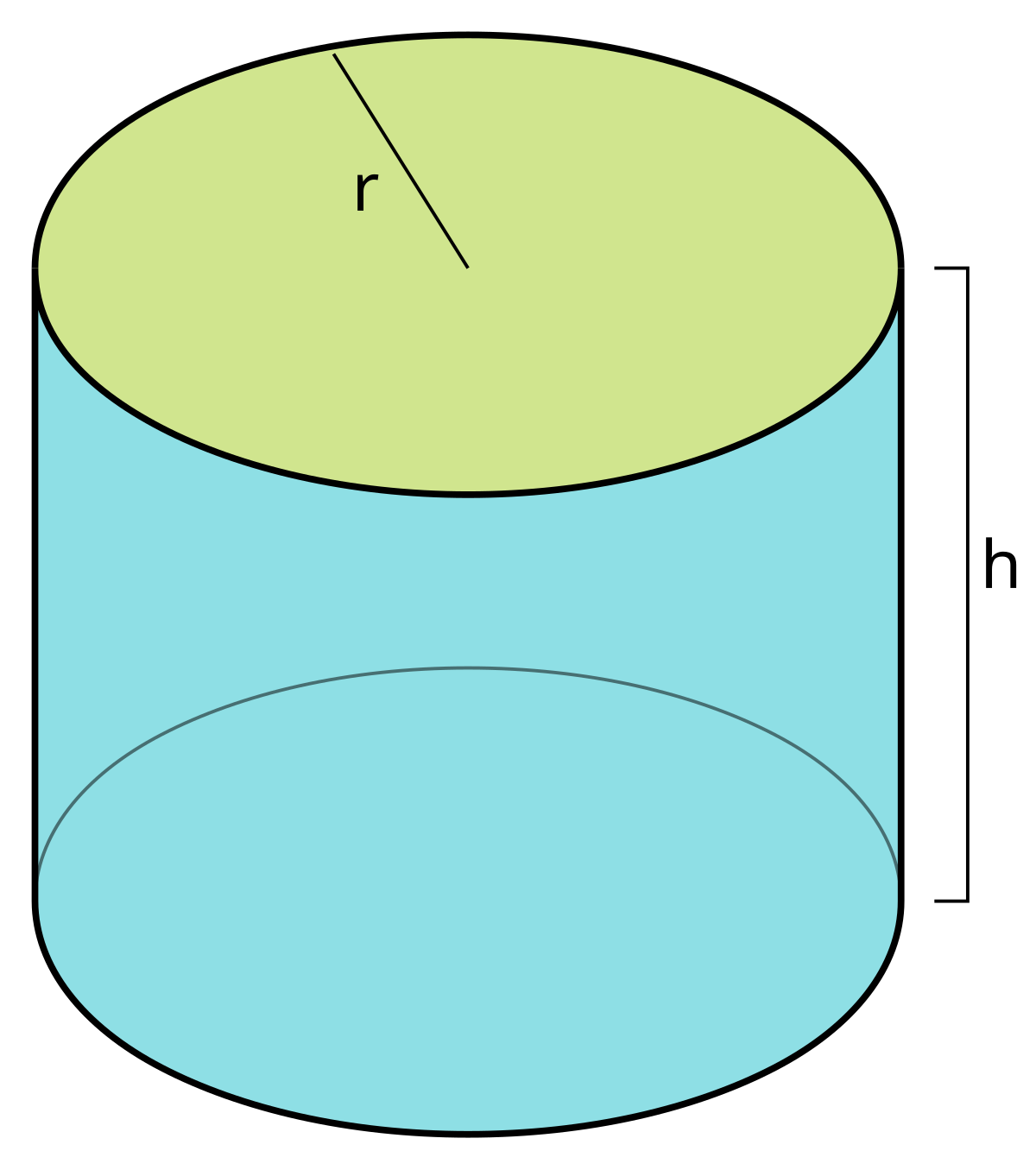
Scrivi la classe Cylinder contenente i metodi seguenti:

public static double getCircumference(double radius): ritorna la circonferenza di un cilindro di raggio radius
public static double getBaseArea(double radius): ritorna l’area di base di un cilindro di raggio radius
public static double getSideArea(double radius, double height): ritorna la superficie laterale di un cilindro di raggio radius e altezza height
public static double getArea(double radius, double height): ritorna l’area totale di un cilindro di raggio radius e altezza height
public static double getVolume(double radius, double height): ritorna il volume di un cilindro di raggio radius e altezza height

Nel metodo main verifica il buon funzionamento di ogni metodo.

Nota: per ottenere il valore di pi-greco puoi utilizzare la costante Math.PI.

Vedi anche wikipedia.

CC BY-SA 3.0, Link

Fibonacci loop math Livello 9

La classe Fibonacci deve generare i primi mille numeri della celeberrima successione di Fibonacci (wiki).

Tale successione inizia con i due valori 0 e 1 (detti F0 e F1). Il valore seguente (F2) si ottiene sommando i due precedenti (0 + 1 = 1), il quarto valore (F3) si ottiene sommado tra loro il F1 e F2 (1 + 1 = 2) e via dicendo. I primi valori della serie sono 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 (F10),…

Bisestili loop math Livello 9

Scrivi il programma Bisestili che stampa tutti gli anni bisestili (wiki) tra il 1600 e il 3000. Esempio:

1600, 1604, 1608, 1612, 1616, 1620, ... 2976, 2980, 2984, 2988, 2992, 2996.

Triangolo methods math Livello 9

Scrivi la classe Triangolo contenente il metodo:

public static double calcolaAreaTriangolo(double base, double altezza)

Tale metodo ritorna un numero che rappresenta l’ area di un triangolo di base base e di altezza altezza.

Cerchio methods math Livello 9

Scrivi la classe Cerchio contenente il metodo:

public static double calcolaCirconferenza(double raggio)

Tale metodo ritorna un numero che rappresenta la circonferenza di un cerchio di raggio raggio.

PerfectNumber array math Livello 10

Scrivi la classe PerfectNumber utile per individuare i numeri perfetti. La classe deve esportare i metodi seguenti:

public static boolean isPerfect(int n): ritorna true se n è un numero perfetto, false altrimenti
public static boolean isDefective(int n): ritorna true se n è un numero difettivo, false altrimenti
public static int[] getDividers(int n): ritorna un array contenente l’elenco dei divisori propri di n
public static long getDividersSum(int[] dividers): ritorna la somma dei numeri contenuti nell’array dividers
public static int[] getPerfectNumbers(int min, int max): ritorna un array contenente l’elenco dei numeri perfetti presenti nell’intervallo [min, max]
public static int[] getDefectiveNumbers(int min, int max): ritorna un array contenente l’elenco dei numeri difettivi presenti nell’intervallo [min, max]
public static int[] getAbundantNumbers(int min, int max): ritorna un array contenente l’elenco dei numeri abbondanti presenti nell’intervallo [min, max]

Numeri perfetti

Un numero N è detto perfetto se la somma dei suoi divisori propri (positivi, N escluso) è pari ad N. Ad esempio 28 è un numero perfetto perché sommando i suoi divisori propri (1, 2, 4, 7 e 14) si ottiene 28.

Invece se la somma dei divisori di N è inferiore al suo valore, N è un numero difettivo, mentre se le somma dei divisori è superiore, N è un numero abbondante.

Randomizer math methods Livello 10

Scrivi il programma Randomizer che, dati tre numeri interi passati come argomenti da linea di comando, genera una serie di numeri casuali (separata ',' e terminata da '.').

I primi due argomenti determinano il range dei valori casuali che verranno generati. Il valore più piccolo non sarà compreso nel range mentre il più grande si.

Il terzo argomento determina il numero di valori da generare.

Ad esempio:

$ java Randomizer 0 4 5

1, 3, 1, 2, 4.

Oppure:

$ java Randomizer 5 1 6

2, 4, 5, 3, 5, 2.

Se il numero di argomenti non è sufficiente il programma deve stampare un messaggio di errore e terminare:

$ java Randomizer 5 

Argomenti insufficienti

Se gli argomenti non sono validi il programma dovrà stampare un messaggio di errore indicando il primo valore errato e terminare:

$ java Randomizer 1 4 b 

Argomento non valido: b

Nota: è vietato utilizzare la classe java.util.Random.

ActionableIsbnChecker string math Livello 10

L’ISBN-13 azionabile è un codice composto secondo il modello:

	ISBN A 10.###.#######/###

Ad esempio:

	ISBN A 10.978.8889637/418

Dove la sequenza di # rappresenta 13 cifre (12 cifre di codice + 1 cifra di controllo).

La cifra di controllo si calcola in base al valore delle 12 cifre precedenti con il seguente algoritmo numerico:

si moltiplica ogni cifra per un peso che assume in modo alternato i valori 1 e 3, partendo dalla prima cifra a sinistra che ha peso 1
si sommano i risultati
si divide la somma per 10 e si prende il resto della divisione
si sottrae il risultato da 10: questa cifra è la cifra di controllo; se quest’ultimo risultato fosse proprio 10, lo si sostituirà con 0.

Ad esempio per il codice ISBN A 10.978.8843025/34:

* 1 + 7 * 3 + 8 * 1 + 8 * 3 + 8 * 1 + 4 * 3 + 3 * 1 + ... + 4 * 3 = 117

diviso 10 da resto 7

- 7 = 3 

la cifra di controllo sarebbe 3 (quindi il codice completo sarebbe ISBN A 10.978.8843025/343).

Scrivi il programma ActionableIsbnChecker che chiede all’utente di inserire un codice ISBN-13 azionabile e ne verifica la correttezza.

I prefissi ISBN, A e 10, i punti, lo slash e gli spazi ('.', '/' e '' ) sono opzionali, se vengono omessi il programma esegue comunque la verifica.

Il codice e la cifra di controllo devono essere presenti e validi, altrimenti il programma stampa un messaggio di errore.

Se il codice non è valido, il messaggio stampato è Codice non valido. Se la cifra di controllo non è valida ([1;10]) il messaggio di errore è Cifra di controllo non valida.

Se l’utente inserisce un codice con il formato ammesso, il programma ne verifica la bontà controllando la corrispondenza tra codice e cifra di controllo. Se corrispondono il programma termina stampando il messaggio Codice verificato!, altrimenti stampa Codice errato.

MathTool math loop methods Livello 10

Scrivi la classe MathTool contenente i metodi:

public static int pow(int base, int exp)

Tale metodo calcola l’elevazione a potenza (base elevato exp).

public static int factorial(int n)

Che ritorna il fattoriale di n. Ad esempio il fattoriale di 3 è 6 (3 * 2 * 1 = 6).

public static int digitAt(long number, int index)

Che ritorna il valore della cifra alla posizione index dentro a number. Ad esempio digitAt(123456, 0) ritorna 1, mentre digitAt(123456, 3) ritorna 4. Per risolvere questo problema è vietato ricorrere alla trasformazione di number in una stringa.

SumTool methods math Livello 10

Scrivi la classe SumTool contenente i metodi seguenti:

int sommaUnivoca(int a, int b, int c): Tale metodo ritorna la somma di a, b e c ma i valori duplicati vengono tralasciati nel calcolo del totale. Ad esempio sommaUnivoca(1,2,3) ritorna 6 mentre sommaUnivoca(1,2,1) ritorna 3.
int sommaTonda(int a, int b, int c): ritorna la somma di a, b e c arrotondata al multiplo di 10 più vicino.

Calcolatrice2 exceptions math Livello 10

Riprendi il tuo codice della classe Calcolatrice e modificalo secondo le specifiche seguenti:

Aggiungere la gestione delle eccezioni.
Permettere il calcolo di espressioni contenenti più operatori (es. 1 + 3 + 5).

DivMul methods math Livello 10

Scrivi la classe DivMul contenente i metodo:

public static int calcolaMCD(int a, int b): calcola il massimo comun divisore di 2 numeri (Wiki: MCD).
public static int calcolaMcm(int a, int b): calcola il minimo comune multiplo di 2 numeri (Wiki: mcm).

ElevazioneAPotenza math loop wrapper Livello 10

Scrivi il programma Java ElevazioneAPotenza che calcola l’elevazione a potenza del valore intero passato come primo argomento per il secondo argomento intero.

Esempio:

> java ElevazioneAPotenza 2 3 
2 ^ 3 = 8

PerfectFinder collections math Livello 11

Scrivi la classe PerfectFinder utile per individuare i numeri perfetti. La classe deve esportare i metodi seguenti:

public static boolean isPerfect(int n): ritorna true se n è un numero perfetto, false altrimenti
public static boolean isDefective(int n): ritorna true se n è un numero difettivo, false altrimenti
public static List<Integer> getDividers(int n): ritorna l’elenco dei divisori propri di n
public static long getDividersSum(List<Integer> dividers): ritorna la somma dei numeri con tenuti nella lista dividers
public static List<Integer> getPerfectNumbers(int min, int max): ritorna l’elenco dei numeri perfetti presenti nell’intervallo [min, max]

Numeri perfetti

Invece se la somma dei divisori di N è inferiore al suo valore, N è un numero difettivo, mentre se le somma dei divisori è superiore, N è un numero abbondante.

Calcolatrice methods math Livello 11

Scrivi la classe Calcolatrice contenente il metodo:

public static int calcola(int a, int b, char operatore)

Tale metodo esegue un’operazione matematica di base sui due numeri a e b. Il valore operatore ('+', '-', '*', '/') definisce l’operazione da eseguire.

Ad esempio l’invocazione calcola(5,2,'+') ritornerà 7 (5+2) mentre l’invocazione calcola(5,2,'*') ritornerà 10 (5*2). Se il parametro operatore contiene un carattere non valido, il metodo ritorna 0.

PoTre math methods Livello 11

Scrivi la classe PoTre contenente il metodo:

public static int pow3(int n)

Il metodo riceve un valore intero n e ritorna il valore di 3 elevato n. Ad esempio pow3(2) ritorna 9.

La classe dovrà anche contenere un metodo main in cui verificare se il metodo pow3 funziona correttamente.

Cerchio draw loop math Livello 13

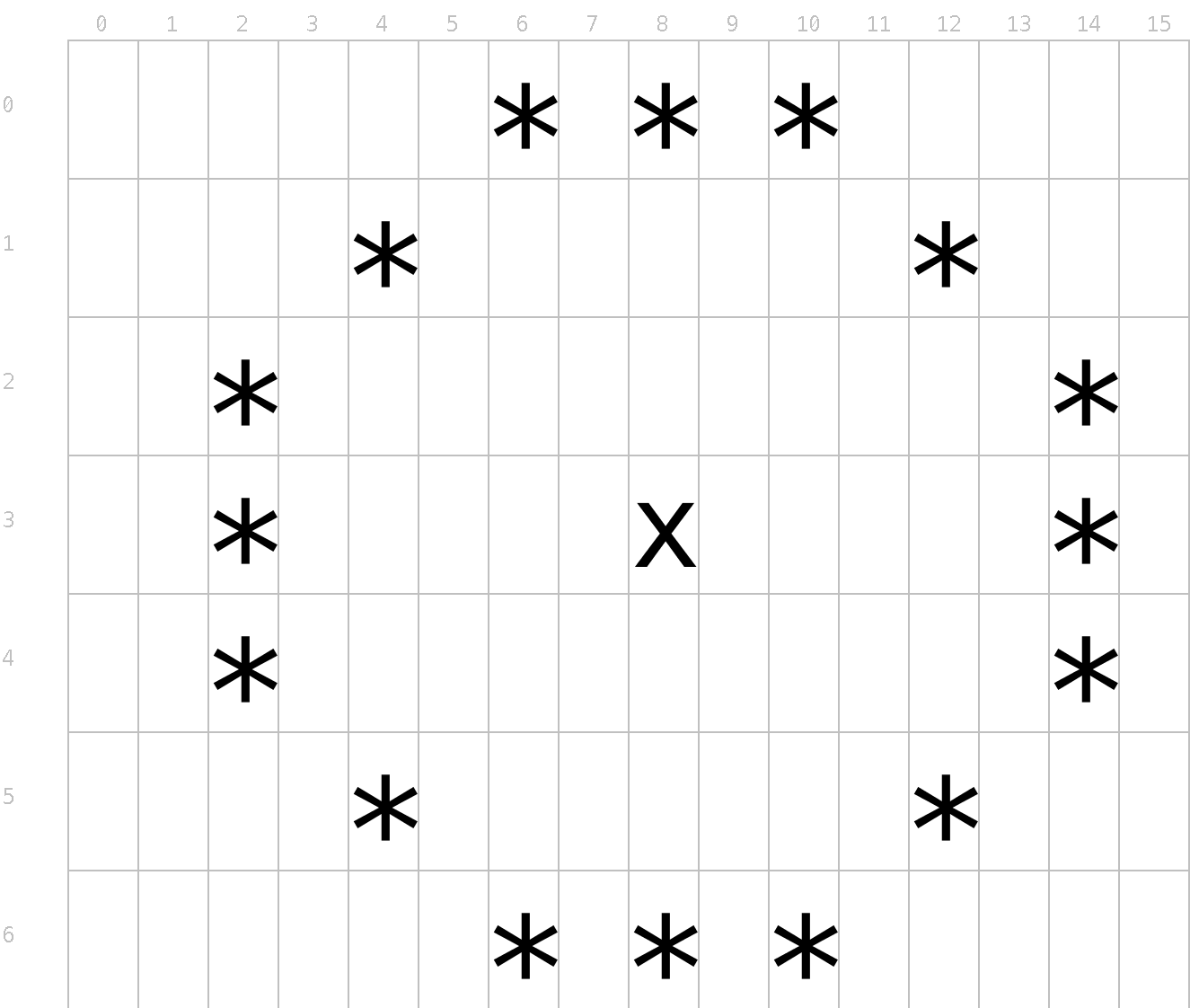
Scrivi il programma Cerchio che chiede all’utente di introdurre un numero intero positivo (N) e poi disegna a terminale un cerchio di raggio pari ad N:

Per N pari a 2 il programma stampa:

    * * *   
  *       * 
  *   x   * 
  *       * 
    * * * 

Per un raggio pari a 3:

      * * *     
    *       *   
  *           * 
  *     x     * 
  *           * 
    *       *   
      * * *  

Per 7:

            * * * * *           
        * *           * *       
      *                   *     
    *                       *   
    *                       *   
  *                           * 
  *                           * 
  *             x             * 
  *                           * 
  *                           * 
    *                       *   
    *                       *   
      *                   *     
        * *           * *       
            * * * * *   

E via dicendo…

Per compensare la forma rettangolare dei caratteri e conferire maggiore rotondità al cerchio, raddoppiare la larghezza del disegno. Ad esempio per un raggio pari a 3: